3.22. PCA¶
In [31]:
import conx as cx
import random
3.22.1. Non-Linearly Separable¶
In [2]:
import math
In [3]:
def distance(x1, y1, x2, y2):
return math.sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
In [4]:
negatives = []
while len(negatives) < 500:
x = random.random()
y = random.random()
d = distance(x, y, 0.5, 0.5)
if d > 0.375 and d < 0.5:
negatives.append([x, y])
positives = []
while len(positives) < 500:
x = random.random()
y = random.random()
d = distance(x, y, 0.5, 0.5)
if d < 0.25:
positives.append([x, y])
In [5]:
symbols = {
"Positive": "bo",
"Negative": "ro"
}
In [6]:
cx.scatter([["Positive", positives],
["Negative", negatives]],
symbols=symbols,
height=6.0, width=6.0)
Out[6]:
In [7]:
net = cx.Network("Non-Linearly Separable", 2, 5, 1, activation="sigmoid")
net.compile(error="mean_absolute_error", optimizer="adam")
In [8]:
net.picture()
Out[8]:
In [9]:
ds = cx.Dataset()
In [10]:
ds.load([(p, [ 1.0], "Positive") for p in positives] +
[(n, [ 0.0], "Negative") for n in negatives])
In [11]:
ds.shuffle()
In [12]:
ds.split(0.1)
In [13]:
net.set_dataset(ds)
In [14]:
net.test(tolerance=0.4)
========================================================
Testing validation dataset with tolerance 0.4...
Total count: 900
correct: 454
incorrect: 446
Total percentage correct: 0.5044444444444445
In [15]:
net.dashboard()
In [16]:
symbols = {
"Positive (correct)": "w+",
"Positive (wrong)": "k+",
"Negative (correct)": "r_",
"Negative (wrong)": "k_",
}
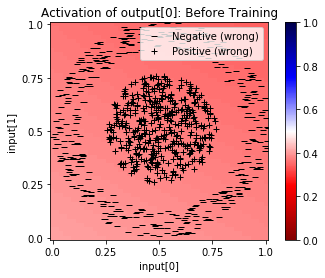
In [17]:
net.plot_activation_map(scatter=net.test(interactive=False), symbols=symbols, title="Before Training")
You may want to either net.reset() or net.retrain() if the
following cell doesn’t complete with 100% accuracy. Calling
net.reset() may be needed if the network has gotten stuck in a local
minimum; net.retrain() may be necessary if the network just needs
additional training.
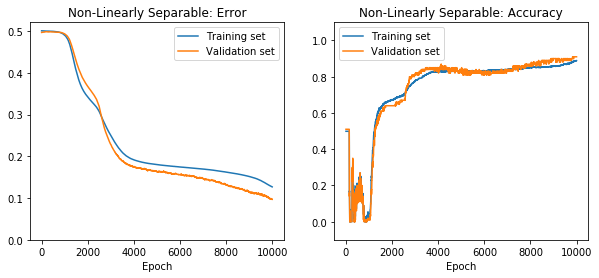
In [18]:
if net.saved():
net.load()
net.plot_results()
else:
net.train(epochs=10000, accuracy=1.0, report_rate=50,
tolerance=0.4, batch_size=128, record=100)
net.save()
In [19]:
cx.scatter(net.test(interactive=False))
Out[19]:
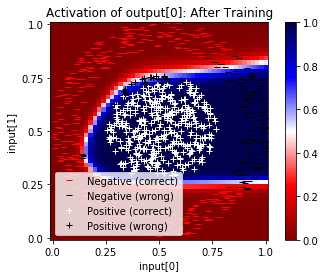
In [20]:
net.plot_activation_map(scatter=net.test(interactive=False), symbols=symbols, title="After Training")
In [21]:
states = [net.propagate_to("hidden", input) for input in net.dataset.inputs]
pca = cx.PCA(states)
In [22]:
symbols = {
"Positive (correct)": "b+",
"Positive (wrong)": "k+",
"Negative (correct)": "r_",
"Negative (wrong)": "k_",
}
In [23]:
pb = net.playback(lambda net,epoch: cx.scatter(**pca.transform_network_bank(net, "hidden", test=True),
symbols=symbols,
title="Epoch %s" % epoch))
pb
In [24]:
pb.goto("end")
In [25]:
movie = net.movie(lambda net,epoch: cx.scatter(**pca.transform_network_bank(net, "hidden", test=True),
symbols=symbols,
format="image",
title="Epoch %s" % epoch),
step=1)
movie
Out[25]:
In [26]:
def function(x, y):
outputs = net.propagate([x, y])
return outputs[0]
In [27]:
cx.heatmap(function)
In [28]:
cx.scatter(**pca.transform_network_bank(net, "hidden", test=True),
symbols=symbols)
Out[28]:
In [29]:
matrix = [[-1 for i in range(50)] for j in range(50)]
for y in cx.frange(0, 1, 0.01):
for x in cx.frange(0, 1, 0.01):
hiddens = net.propagate_to("hidden", [x, y])
vector = pca.transform_one(hiddens, scale=True)
try:
matrix[int(vector[1] * 50)][int(vector[0] * 50)] = net.propagate([x, y])[0]
except:
pass
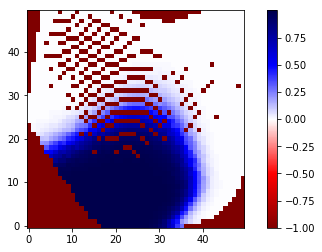
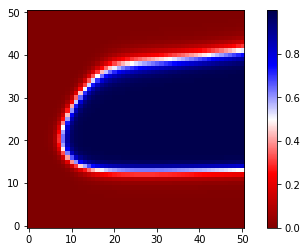
In [30]:
cx.heatmap(matrix)