3.14. Activation Functions¶
This notebook explores the activation functions that are available in Conx.
First, we import a special function plot_f that is designed to plot
functions. We also import all of the activation functions:
- softmax
- elu
- selu
- softplus
- softsign
- relu
- tanh
- sigmoid
- hard_sigmoid
- linear
There are additional advanced activation functions not defined and examined here, including:
- ThresholdedReLU - Thresholded Rectified Linear Unit
- LeakyReLU - Leaky version of a Rectified Linear Unit
- PReLU - Parametric Rectified Linear Unit
In [42]:
from conx.activations import *
import conx as cx
3.14.1. softmax¶
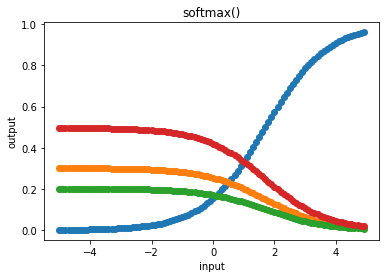
The softmax activation function takes a vector of input values and
returns a vector of output values. This function is unique in that the
output values are not computed independently of one another.
Mathematically, the outputs of softmax always sum to exactly one, but in
practice the sum of the output values will be close to but not exactly
equal to one. The outputs of softmax can be interpreted as
probabilities, and can be used, for example, with Conx’s choice
function.
In [2]:
help(softmax)
Help on function softmax in module conx.activations:
softmax(tensor, axis=-1)
Softmax activation function.
>>> len(softmax([0.1, 0.1, 0.7, 0.0]))
4
In [3]:
softmax([0.1, 0.1, 0.7, 0.0])
Out[3]:
[0.21155263483524323,
0.21155263483524323,
0.38547399640083313,
0.19142073392868042]
In [4]:
sum(softmax([0.1, 0.1, 0.7, 0.0]))
Out[4]:
1.0
In [5]:
softmax([1, 2, 3, 4])
Out[5]:
[0.03205860033631325,
0.08714431524276733,
0.23688282072544098,
0.6439142823219299]
In [6]:
sum(softmax([1, 2, 3, 4]))
Out[6]:
1.0000000186264515
In [7]:
cx.choice(['a', 'b', 'c', 'd'], p=softmax([0.1, 0.1, 0.7, 0.0]))
Out[7]:
'a'
Let’s see how softmax can be used to make probabilistic choices, and see if they match our expectations:
In [8]:
bin = [0] * 4
for x in range(100):
pick = cx.choice([0, 1, 2, 3], p=softmax([0.1, 0.1, 0.7, 0.0]))
bin[pick] += 1
print("softmax:", softmax([0.1, 0.1, 0.7, 0.0]))
print("picks :", [b/100 for b in bin])
softmax: [0.21155263483524323, 0.21155263483524323, 0.38547399640083313, 0.19142073392868042]
picks : [0.22, 0.26, 0.35, 0.17]
In [9]:
f = lambda x: softmax([x, 0.5, 0.1, 1])
In [10]:
cx.plot_f(f, frange=(-5, 5, 0.1), xlabel="input", ylabel="output", title="softmax()")
3.14.2. elu¶
In [11]:
help(elu)
Help on function elu in module conx.activations:
elu(x, alpha=1.0)
Exponential Linear Unit activation function.
See: https://arxiv.org/abs/1511.07289v1
def elu(x):
if x >= 0:
return x
else:
return alpha * (math.exp(x) - 1.0)
>>> elu(0.0)
0.0
>>> elu(1.0)
1.0
>>> elu(0.5, alpha=0.3)
0.5
>>> round(elu(-1), 1)
-0.6
In [12]:
elu(0.5)
Out[12]:
0.5
In [13]:
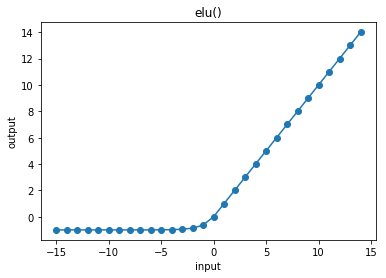
cx.plot_f(elu, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="elu()")
In [14]:
elu(0.5, .3)
Out[14]:
0.5
In [15]:
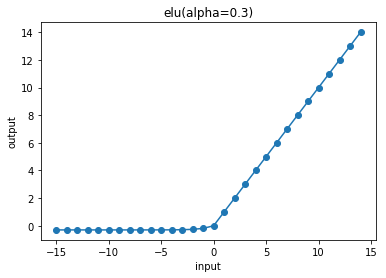
cx.plot_f(lambda x: elu(x, 0.3), frange=(-15, 15, 1), xlabel="input", ylabel="output", title="elu(alpha=0.3)")
3.14.3. selu¶
In [16]:
help(selu)
Help on function selu in module conx.activations:
selu(x)
Scaled Exponential Linear Unit activation function.
>>> selu(0)
0.0
In [17]:
selu(0.5)
Out[17]:
0.5253505110740662
In [18]:
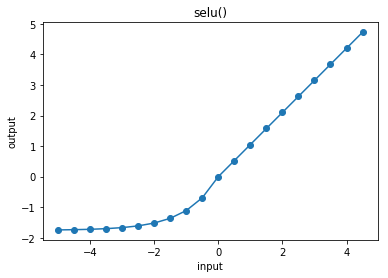
cx.plot_f(selu, frange=(-5, 5, 0.5), xlabel="input", ylabel="output", title="selu()")
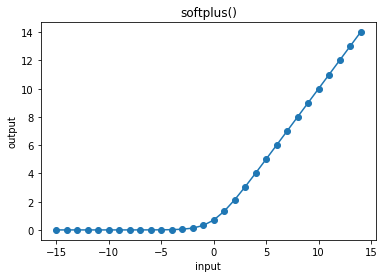
3.14.4. softplus¶
In [19]:
help(softplus)
Help on function softplus in module conx.activations:
softplus(x)
Softplus activation function.
>>> round(softplus(0), 1)
0.7
In [20]:
softplus(0.5)
Out[20]:
0.9740769863128662
In [21]:
cx.plot_f(softplus, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="softplus()")
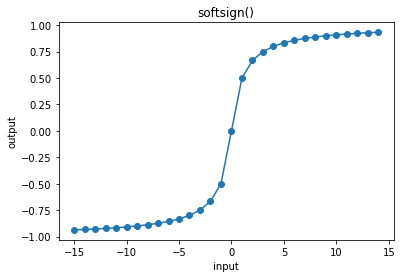
3.14.5. softsign¶
In [22]:
help(softsign)
Help on function softsign in module conx.activations:
softsign(x)
Softsign activation function.
>>> softsign(1)
0.5
>>> softsign(-1)
-0.5
In [23]:
softsign(0.5)
Out[23]:
0.3333333432674408
In [24]:
cx.plot_f(softsign, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="softsign()")
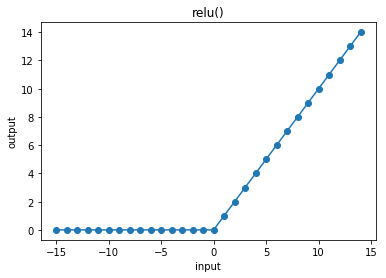
3.14.6. relu¶
In [25]:
help(relu)
Help on function relu in module conx.activations:
relu(x, alpha=0.0, max_value=None)
Rectified Linear Unit activation function.
>>> relu(1)
1.0
>>> relu(-1)
0.0
In [26]:
relu(0.5)
Out[26]:
0.5
In [27]:
cx.plot_f(relu, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="relu()")
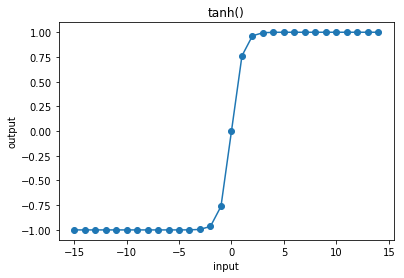
3.14.7. tanh¶
In [28]:
help(tanh)
Help on function tanh in module conx.activations:
tanh(x)
Tanh activation function.
>>> tanh(0)
0.0
In [29]:
tanh(0.5)
Out[29]:
0.46211716532707214
In [30]:
cx.plot_f(tanh, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="tanh()")
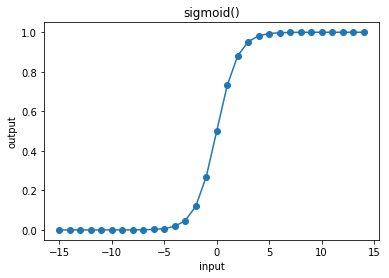
3.14.8. sigmoid¶
In [31]:
help(sigmoid)
Help on function sigmoid in module conx.activations:
sigmoid(x)
Sigmoid activation function.
>>> sigmoid(0)
0.5
In [32]:
sigmoid(0.5)
Out[32]:
0.622459352016449
In [33]:
cx.plot_f(sigmoid, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="sigmoid()")
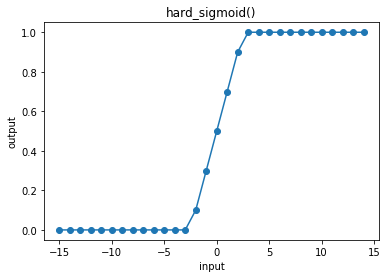
3.14.9. hard_sigmoid¶
In [34]:
help(hard_sigmoid)
Help on function hard_sigmoid in module conx.activations:
hard_sigmoid(x)
Hard Sigmoid activation function.
>>> round(hard_sigmoid(-1), 1)
0.3
In [35]:
hard_sigmoid(0.5)
Out[35]:
0.6000000238418579
In [36]:
cx.plot_f(hard_sigmoid, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="hard_sigmoid()")
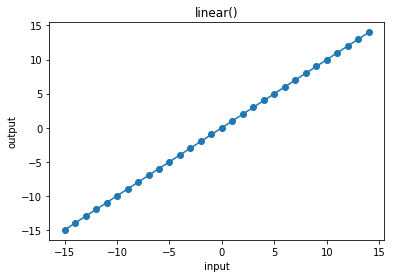
3.14.10. linear¶
In [37]:
help(linear)
Help on function linear in module conx.activations:
linear(x)
Linear activation function.
>>> linear(1) == 1
True
>>> linear(-1) == -1
True
In [38]:
linear(0.5)
Out[38]:
0.5
In [39]:
cx.plot_f(linear, frange=(-15, 15, 1), xlabel="input", ylabel="output", title="linear()")
3.14.11. Comparison¶
In [40]:
functions = [hard_sigmoid, sigmoid, tanh, relu,
softsign, softplus, elu, selu, linear]
float_range = cx.frange(-2, 2, 0.1)
lines = {}
symbols = {}
for v in float_range:
for f in functions:
if f.__name__ not in lines:
lines[f.__name__] = []
symbols[f.__name__] = "-"
lines[f.__name__].append(f(v))
In [41]:
cx.plot(list(lines.items()), xs=float_range, symbols=symbols, height=6.0, width=8.0,
title="Activation Functions", xlabel="input", ylabel="output")
Out[41]:
See also the advanced activation functions: