3.8. Plotting

This notebook demonstrates some of Conx’s functions for visualizing the behavior of networks. First, let’s create a simple XOR network to explore.

In [1]:

import conx as cx

Using TensorFlow backend.
Conx, version 3.6.1

In [2]:

net = cx.Network("XOR 2-3-1 Network")
net.add(cx.Layer("input", shape=2))
net.add(cx.Layer("hidden", shape=3, activation='sigmoid'))
net.add(cx.Layer("output", shape=1, activation='sigmoid'))
net.connect()

XOR = [
    ([0, 0], [0], "1"),
    ([0, 1], [1], "2"),
    ([1, 0], [1], "3"),
    ([1, 1], [0], "4")
]
net.dataset.load(XOR)
net.dataset.info()

net.compile(loss='mean_squared_error', optimizer='sgd', lr=0.3, momentum=0.9)

Dataset: Dataset for XOR 2-3-1 Network

Information: * name : None * length : 4

Input Summary: * shape : (2,) * range : (0.0, 1.0)

Target Summary: * shape : (1,) * range : (0.0, 1.0)

In [3]:

net.picture()

Out[3]:
Layer: output (output) output range: (0, 1) shape = (1,) Keras class = Dense activation = sigmoidoutputWeights from hidden to output output/kernel:0 has shape (3, 1) output/bias:0 has shape (1,)Layer: hidden (hidden) output range: (0, 1) shape = (3,) Keras class = Dense activation = sigmoidhiddenWeights from input to hidden hidden/kernel:0 has shape (2, 3) hidden/bias:0 has shape (3,)Layer: input (input) output range: (0.0, 1.0) shape = (2,) Keras class = InputinputXOR 2-3-1 Network
In [4]:

cx.view(net.get_weights_as_image("hidden"))
_images/Plotting_5_0.png 
In [8]:

net.plot_layer_weights('hidden', colormap="RdBu"
_images/Plotting_6_0.png 
In [6]:

net.train(epochs=1000, accuracy=1, report_rate=25, record=True)
_images/Plotting_7_0.svg
========================================================
       |  Training |  Training
Epochs |     Error |  Accuracy
------ | --------- | ---------
#  533 |   0.00652 |   1.00000

In [7]:

net.plot('loss', ymin=0)
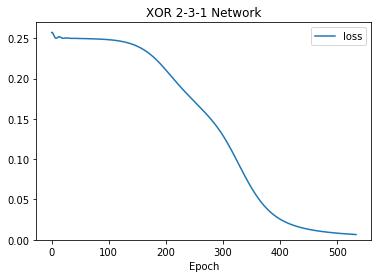
_images/Plotting_8_0.png

3.8.1. plot_activation_map

This plotting function allows us to see the activation of a specific unit in a specific layer, as a function of the activations of two other units from an earlier layer. In this example, we show the behavior of the single output unit as the two input units are varied across the range 0.0 to 1.0:

In [8]:

net.plot_activation_map('input', (0,1), 'output', 0)
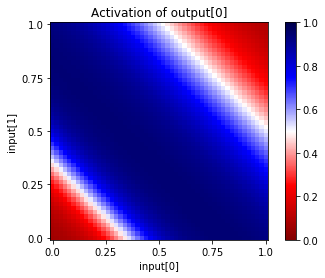
_images/Plotting_10_0.png

We can verify the above output activation map by running different input vectors through the network manually:

In [9]:

print(net.propagate([0,0])[0])
print(net.propagate([1,1])[0])
print(net.propagate([0.5, 0.5])[0])
print(net.propagate([0, 0.6])[0])

0.06735210865736008
0.09960916638374329
0.9248424768447876
0.8984166383743286

In [10]:

# map of hidden[2] activation as a function of the inputs
net.plot_activation_map('input', (0,1), 'hidden', 2, show_values=True)
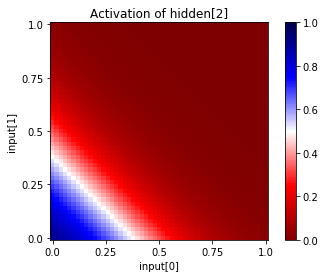
_images/Plotting_13_0.png 
----------------------------------------------------------------------------------------------------
Activation of hidden[2] as a function of input[0] and input[1]
rows: input[1] decreasing from 1.00 to 0.00
cols: input[0] increasing from 0.00 to 1.00

0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.04 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.05 0.04 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.06 0.05 0.04 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.09 0.06 0.05 0.04 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.11 0.09 0.06 0.05 0.04 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.15 0.11 0.08 0.06 0.05 0.04 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.19 0.15 0.11 0.08 0.06 0.05 0.04 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00 0.00
0.24 0.19 0.15 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00 0.00
0.30 0.24 0.19 0.15 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00 0.00
0.37 0.30 0.24 0.19 0.14 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00 0.00
0.44 0.37 0.30 0.24 0.19 0.14 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00 0.00
0.52 0.44 0.37 0.30 0.24 0.19 0.14 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01 0.01 0.00 0.00
0.59 0.52 0.44 0.37 0.30 0.24 0.19 0.14 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01 0.01 0.00
0.67 0.59 0.52 0.44 0.37 0.30 0.24 0.18 0.14 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01 0.01
0.73 0.67 0.59 0.52 0.44 0.36 0.30 0.24 0.18 0.14 0.11 0.08 0.06 0.05 0.03 0.03 0.02 0.01 0.01 0.01
0.79 0.73 0.66 0.59 0.52 0.44 0.36 0.30 0.23 0.18 0.14 0.11 0.08 0.06 0.05 0.03 0.02 0.02 0.01 0.01
0.83 0.79 0.73 0.66 0.59 0.51 0.44 0.36 0.29 0.23 0.18 0.14 0.11 0.08 0.06 0.05 0.03 0.02 0.02 0.01
0.87 0.83 0.78 0.73 0.66 0.59 0.51 0.44 0.36 0.29 0.23 0.18 0.14 0.11 0.08 0.06 0.05 0.03 0.02 0.02
0.90 0.87 0.83 0.78 0.73 0.66 0.59 0.51 0.43 0.36 0.29 0.23 0.18 0.14 0.11 0.08 0.06 0.04 0.03 0.02
----------------------------------------------------------------------------------------------------

In [11]:

# map of output activation as a function of hidden units 1,2
net.plot_activation_map('hidden', (1,2), 'output', 0)
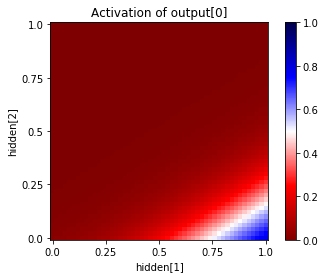
_images/Plotting_14_0.png

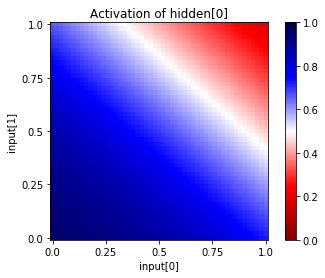
How does the network actually solve the problem? We can look at the intermediary values at the hidden layer by plotting each of the 4 hidden units in this manner:

In [12]:

net.plot_activation_map('input', (0,1), 'hidden', 0)
_images/Plotting_16_0.png 
In [13]:

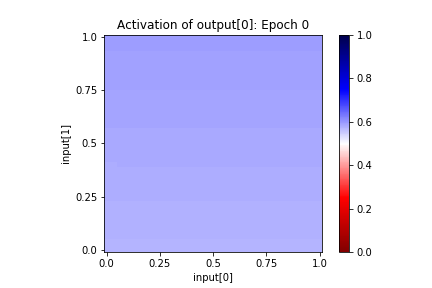
net.playback(lambda net,epoch: net.plot_activation_map(title="Epoch %s" % epoch, format='image'))
_images/Plotting_17_1.png

3.8.2. Adding Additional Hidden Layers

In [14]:

net = cx.Network("XOR 2-3-2-1 Network")
net.add(cx.Layer("input", shape=2))
net.add(cx.Layer("hidden", shape=3, activation='sigmoid'))
net.add(cx.Layer("hidden2", shape=2, activation='sigmoid'))
net.add(cx.Layer("output", shape=1, activation='sigmoid'))
net.connect()

XOR = [
    ([0, 0], [0], "1"),
    ([0, 1], [1], "2"),
    ([1, 0], [1], "3"),
    ([1, 1], [0], "4")
]
net.compile(loss='mean_squared_error', optimizer='sgd', lr=0.3, momentum=0.9)
net.dataset.load(XOR)

In [15]:

net.reset()
net.train(epochs=2000, accuracy=1, report_rate=25)
_images/Plotting_20_0.svg
========================================================
       |  Training |  Training
Epochs |     Error |  Accuracy
------ | --------- | ---------
#  886 |   0.00721 |   1.00000

In [16]:

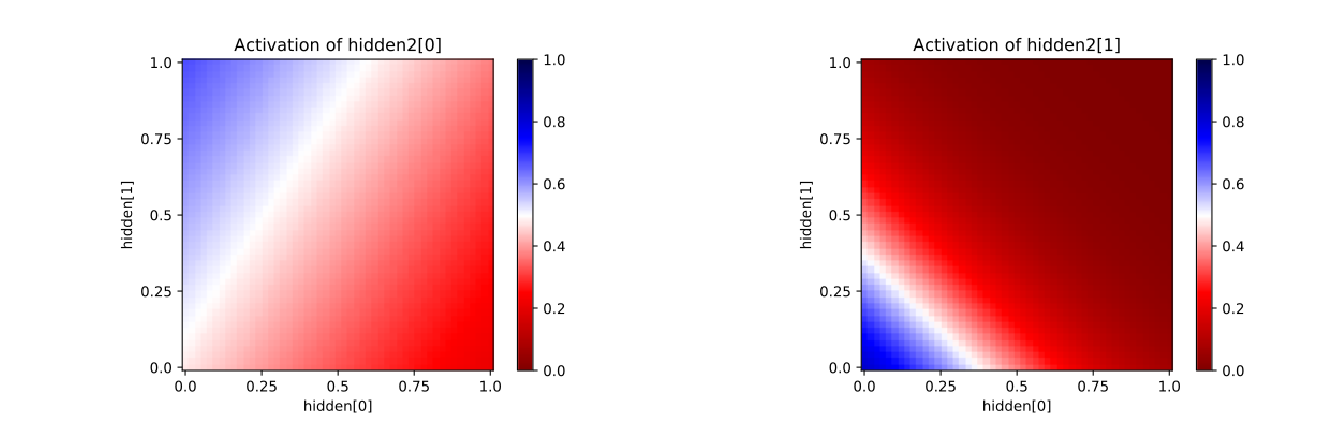
#net.plot_activation_map('hidden', (0,1), 'hidden2', 1)
cx.view([net.plot_activation_map('hidden', (0,1), 'hidden2', i, format='svg') for i in range(2)], scale=10)
_images/Plotting_21_0.png

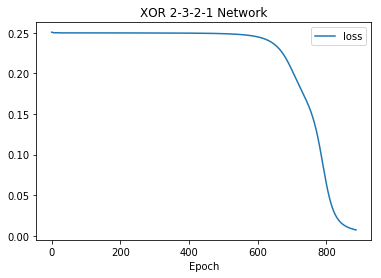
3.8.3. Plotting training error (loss) and training accuracy (acc)

In [17]:

net.plot("loss")
_images/Plotting_23_0.png 
In [18]:

net.plot("acc")
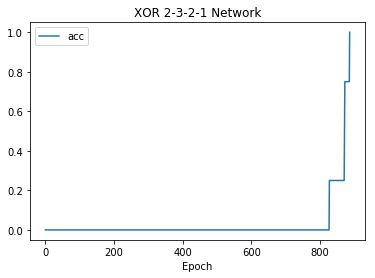
_images/Plotting_24_0.png 
In [19]:

net.plot(["loss", "acc"])
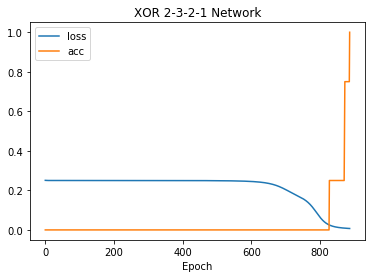
_images/Plotting_25_0.png 
In [20]:

net.plot("all")
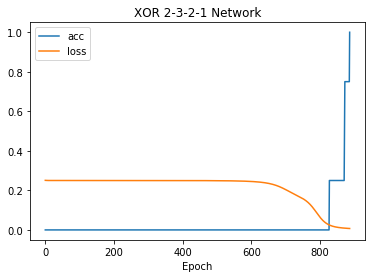
_images/Plotting_26_0.png

3.8.4. Plotting Your Own Data

In [21]:

data = ["Type 1", [(0, 1), (1, 2), (2, .5)]]
cx.scatter(data)

Out[21]:
_images/Plotting_28_0.svg
In [22]:

data = ["My Data", [1, 2, 6, 3, 4, 1]]
symbols = {"My Data": "rx"}
cx.plot(data, symbols=symbols)

Out[22]:
_images/Plotting_29_0.svg
In [23]:

data = [["My Data", [1, 2, 6, 3, 4, 1]],
        ["Your Data", [2, 4, 5, 1, 2, 6]]]
symbols = {"My Data": "rx-", "Your Data": "bo-"}
cx.plot(data, symbols=symbols)

Out[23]:
_images/Plotting_30_0.svg