2. Getting Started with ConX¶
2.1. What is ConX?¶
ConX is an accessible and powerful way to build and understand deep learning neural networks. Specifically, it sits on top of Keras, which sits on top of TensorFlow, CNTK, or Theano (though Theano is no longer being developed).
ConX:
- has an easy to use interface for creating connections between layers of a neural network
- adds additional functionality for manipulating neural networks
- supports visualizations and analysis for training and using neural networks
- has everything you need; doesn’t require knowledge of complicated numerical or plotting libraries
- integrates with lower-level (Keras) if you wish
But rather than attempting to explain each of these points, let’s demonstrate them. There are 8 steps needed to construct and use a ConX network:
- import conx
- create the network
- add desired layers
- connect the layers
- compile the network, with a loss function and optimizer method
- create a dataset
- train the network
- test/analyze the network
This demonstration is being run in a Jupyter Notebook. ConX doesn’t require running in the notebook, but if you do, you will be able to use the visualizations and dashboard.
2.2. A Simple Network¶
As a demonstration, let’s build a simple network for learning the XOR (exclusive or). XOR is defined as:
| Input 1 | Input 2 | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2.2.1. Step 1: import conx¶
We will need the Network, and Layer classes from the conx module:
[1]:
import conx as cx
Using TensorFlow backend.
ConX, version 3.7.4
2.2.3. Step 3: add the needed layers¶
Every layer needs a name and a size. We add each of the layers of our network. The first layer will be an “input” layer (named arbitrarily “input”). We only need to specify the size. For our XOR problem, there are two inputs:
[3]:
net.add(cx.Layer("input", 2))
[3]:
'input'
For the next layers, we will also use the default layer type for hidden and output layers. However, we also need to specify the function to apply to the “net inputs” to the layer, after the matrix multiplications. We have a few choices for which activation functions to use:
- ‘relu’
- ‘sigmoid’
- ‘linear’
- ‘softmax’
- ‘tanh’
- ‘elu’
- ‘selu’
- ‘softplus’
- ‘softsign’
- ‘hard_sigmoid’
You can try any of these, though the sigmoid function generally works best for this problem. Feel free to experiment with other options.
[4]:
net.add(cx.Layer("hidden", 3, activation="sigmoid"))
net.add(cx.Layer("output", 1, activation="sigmoid"))
[4]:
'output'
2.2.4. Step 4: connect the layers¶
We connect up the layers as needed. This is a simple 3-layer network:
[5]:
net.connect("input", "hidden")
net.connect("hidden", "output")
Note:
We use the term layer here because each of these items composes the layer itself. In general though, a layer can be composed of many of these items. In that case, we call such a layer a bank.
2.2.5. Step 5: compile the network¶
Before we can do this step, we need to do two things:
- tell the network how to compute the error between the targets and the actual outputs
- tell the network how to adjust the weights when learning
2.2.5.1. Error (or loss)¶
The first option is called the error (or loss). There are many choices for the error function, and we’ll dive into each later. For now, we’ll just briefly mention them:
- “mse” - mean square error
- “mae” - mean absolute error
- “mape” - mean absolute percentage error
- “msle” - mean squared logarithmic error
- “kld” - kullback leibler divergence
- “cosine” - cosine proximity
2.2.5.2. Optimizer¶
The second option is called “optimizer”. Again, there are many choices, but we just briefly name them here:
- “sgd” - Stochastic gradient descent optimizer
- “rmsprop” - RMS Prop optimizer
- “adagrad” - ADA gradient optimizer
- “adadelta” - ADA delta optimizer
- “adam” - Adam optimizer
- “adamax” - Adamax optimizer from Adam
- “nadam” - Nesterov Adam optimizer
- “tfoptimizer” - a native TensorFlow optimizer
For now, we’ll just pick “mse” for the error function, and “adam” for the optimizer.
And we compile the network:
[6]:
net.compile(error="mse", optimizer="sgd", lr=0.1, momentum=0.5)
2.2.5.3. Option: inspect the initial weights¶
Networks in ConX are initialized with small random weights in the range -1..1. Each unit in a layer is also give a bias, which is initialized to 0. A bias is trained, just as the weights, and is added in when calculating a unit’s incoming activation. Once trained, the bias provides each unit with a default activation value in the absence of other inputs.
You can inspect the weights coming into a layer, as shown below.
[7]:
net.get_weights("hidden")
[7]:
[[[-0.767471432685852, 0.10572397708892822, -0.7625459432601929],
[-0.6755458116531372, 0.20516455173492432, 0.43674349784851074]],
[0.0, 0.0, 0.0]]
[8]:
net.get_weights("output")
[8]:
[[[0.471946120262146], [0.9158862829208374], [1.1649702787399292]], [0.0]]
2.2.5.4. Option: visualize the network¶
At this point in the steps, you can see a visual representation of the network by simply asking for a picture:
[9]:
net.picture()
[9]:
This is useful to see the layers and connections.
Propagating the network places an array on the input layer, and sends the values through the network. We can try any input vector:
[10]:
net.propagate([-2, 2])
[10]:
[0.8616290092468262]
If we would like to see the activations on all of the units in the network, we can take a picture with the same input vector. You should show some colored squares in the layers representing the activation levels at each unit:
[11]:
net.picture([-2, 2])
[11]:
In these visualizations, the color gives an indication of its relative activation value of each neuron.
For input layers, the default is to give a gray scale value representing the possible ranges, black meaning negative and white meaning more positive.
For non-input layers, the more red a unit is, the smaller its value, and the more blue, the larger its value. Values close to zero will appear whiter.
Notice that if you propagate this untrained network with zeros, then the hidden layer activations are all white. This means that there is no activation at any node in the network. This is because the bias units are initialized at zero.
[12]:
net.propagate([0,0])
[12]:
[0.7818366289138794]
[13]:
net.picture([0,0])
[13]:
2.2.6. Step 6: setup the training data¶
For this little experiment, we want to train the network on our table from above. To do that, we add the inputs and the targets to the dataset, one at a time:
[14]:
net.dataset.append([0, 0], [0])
net.dataset.append([0, 1], [1])
net.dataset.append([1, 0], [1])
net.dataset.append([1, 1], [0])
[15]:
net.dataset.info()
Dataset: Dataset for XOR Network
Information: * name : None * length : 4
Input Summary: * shape : (2,) * range : (0.0, 1.0)
Target Summary: * shape : (1,) * range : (0.0, 1.0)
2.2.7. Step 7: train the network¶
[16]:
net.reset()
[17]:
net.train(epochs=5000, accuracy=1.0, tolerance=0.2, report_rate=100)
========================================================
| Training | Training
Epochs | Error | Accuracy
------ | --------- | ---------
# 4531 | 0.02997 | 1.00000
Perhaps the network learned none, some, or all of the patterns. You can reset the network, and try again, by re-running the above cell.
2.2.8. Step 8: test the network¶
[18]:
net.evaluate(show=True)
========================================================
Testing validation dataset with tolerance 0.2...
# | inputs | targets | outputs | result
---------------------------------------
0 | [[0.00, 0.00]] | [[0.00]] | [0.13] | correct
1 | [[0.00, 1.00]] | [[1.00]] | [0.82] | correct
2 | [[1.00, 0.00]] | [[1.00]] | [0.82] | correct
3 | [[1.00, 1.00]] | [[0.00]] | [0.20] | correct
Total count: 4
correct: 4
incorrect: 0
Total percentage correct: 1.0
2.2.9. The dashboard¶
The dashboard allows you to interact, test, and generally work with your network via a GUI.
[19]:
net.dashboard()
ConX has a number of methods for visualizing images. In this example below, we get each picture of the network as an “image” and give the list of images to cx.view.
[20]:
for i in range(4):
display(net.picture(net.dataset.inputs[i], scale=0.15))
2.3. ConX options¶
2.3.1. Propagation functions¶
There are five ways to propagate activations through the network:
- Network.propagate(
inputs) - propagate these inputs through the network - Network.propagate_to(
inputs) - propagate these inputs to this bank (returns the output at that layer) - Network.propagate_from(
bank-name,activations) - propagate the activations frombank-nameto outputs - Network.propagate_to_image(
bank-name,activations, scale=SCALE) - returns an image of the layer activations - Network.propagate_to_features(
bank-name,activations, scale=SCALE) - gets a matrix of images for each feature (channel) at the layer
[22]:
net.propagate_from("hidden", [0, 1, 0])
[22]:
[0.0340755395591259]
[23]:
net.propagate_to("hidden", [0.5, 0.5])
[23]:
[0.2813264727592468, 0.031041061505675316, 0.1953100860118866]
[24]:
net.propagate_to("hidden", [0.1, 0.4])
[24]:
[0.36196693778038025, 0.26838693022727966, 0.06002996116876602]
There is also a propagate_to_image() that takes a bank name, and inputs.
[25]:
net.propagate_to_image("hidden", [0.1, 0.4]).resize((500, 100))
[25]:

2.3.2. Plotting options¶
You can re-plot the plots from the entire training history with:
[26]:
net.plot_results()
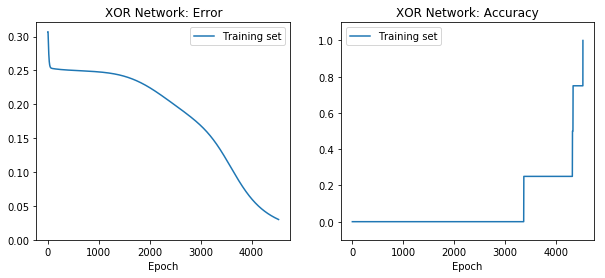
You can plot the following values from the training history:
- “loss” - error measure (eg, “mse”, mean square error)
- “acc” - the accuracy of the training set
You can plot any subset of the above on the same plot:
[27]:
net.plot(["acc", "loss"])
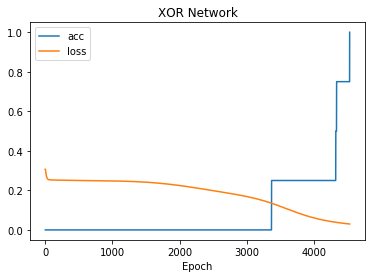
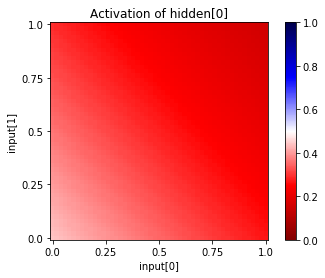
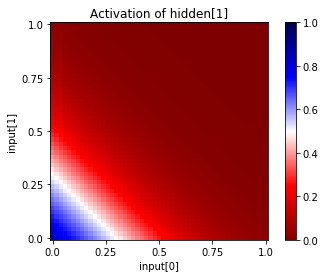
You can also see the activations at a particular unit, given a range of input values for two input units. Since this network has only two inputs, and one output, we can see the entire input and output ranges:
[28]:
for i in range(net["hidden"].size):
net.plot_activation_map(from_layer="input", from_units=(0,1),
to_layer="hidden", to_unit=i)
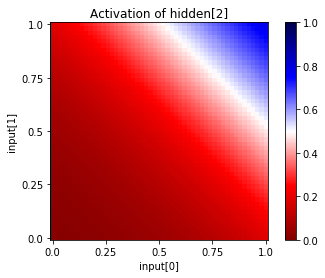
[29]:
net.plot_activation_map(from_layer="input", from_units=(0,1),
to_layer="output", to_unit=0)
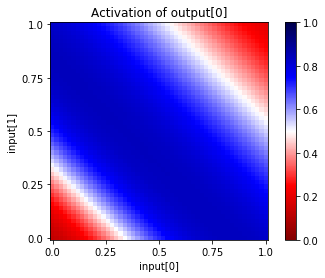
[30]:
net.plot_activation_map()
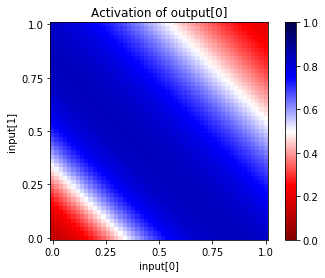
[ ]: